一日以上風が吹き続け、コリオリ力の影響が無視できなくなったとき、海面を吹く風によって、海にはどのような流れが生じるだろうか。
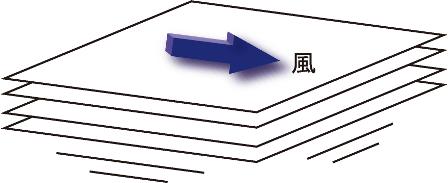
いきなり流体を考えるとややこしい。下図のような簡単なモデルから始めよう。上下に重なった無限に広い板の上に風が吹いている。そして風は、一番上の板を、風の吹き去る方向に引きずっている。
エクマン理論
一日以上風が吹き続け、コリオリ力の影響が無視できなくなったとき、海面を吹く風によって、海にはどのような流れが生じるだろうか。
いきなり流体を考えるとややこしい。下図のような簡単なモデルから始めよう。上下に重なった無限に広い板の上に風が吹いている。そして風は、一番上の板を、風の吹き去る方向に引きずっている。

最初はコリオリ力の効果を考えない(非回転系)での板の動きを考えよう。

一番上の板には、風が引きずる力(A1; 以降、風応力)が図の右向きに働いている。これによって板は紫矢印の向きに動き始める。同時に、下の板との摩擦力(B1)が、板の移動方向と逆向き(図の左向き)に働きだす。
一番上の板が動くことで、摩擦力(A2=B1)が二番目の板に伝わり、これによって二番目の板も、右方向に動きだす。同時に、三番目の板との摩擦力(B2)が、板の移動方向と逆向き(図の左向き)に働く。
以降、繰り返し。上下に重なった板は、下に行くほど速度を弱めつつ、風と同じ方向へ移動していく。
結局、非回転系での板は、下図左のように、風と同じ方向に、下へ行くほど速度を弱めて動くようになるだろう。水を「極限にまで薄くした板が、無限枚重なったもの」と考えれば、結局、海の上に風が吹く場合も同じこと。これは日常的な感覚とも一致しやすい。
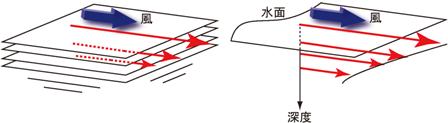
つづいて、風が、一日程度以上、同じ方向に吹き続けた場合の海水の動きを考える。コリオリ力の効果を考える回転系の場合である。
●板に働く力は、三つになる。風の吹く方向に働く風応力(上のA)、板の動く方向と逆向きに働く摩擦力(B)**注、そして北半球で板の動く方向に対して直角右向きに働くコリオリ力(以降、Cで表記)である。それぞれ、働く方向には決められたルールがあることに注意。
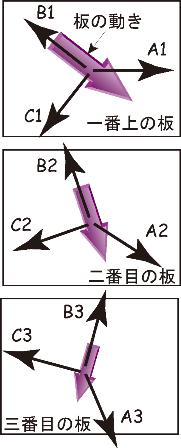
一番上の板には、風の方向に働く風応力(A1)が働いている。これとバランスするのは、板の動きと逆向きに働く、下の板との摩擦力(B1)と、板の動きの直角右向きに働くコリオリ力(C1)である。働く方向に決められたルールを守りつつ、三つ力がバランスするためには、板は紫矢印のように、風の吹き去る方向より右にずれる必要がある(正確には0度以上90度未満で。A1の大きさによって角度は変わる)。
一番上の板が動けば、同じ方向に摩擦力(A2=B1)が二番目の板に伝わり、これによって二番目の板も動きだす。同時に、働く方向に決められたルールを守りつつ、三つ力がバランスするためには、二番目の板は、紫矢印のように、一番目の板の動く方向(A2の方向)より、さらに右にずれる必要がある。
以降、繰り返し。上下に重なった板は、下に行くほど速度を弱めつつ移動していく。ただし移動する向きは、下へゆくにしたがい、右へ右へと、ずれていく。
結局、回転系での板の動きは、下図左のように、風方向から、下へ行くほど右にずれつつ、また速度を弱めつつ動くようになるだろう。水を「極限にまで薄くした板が、無限枚重なったもの」と考えれば、結局、海の上に風が吹く場合も同じこと。

風によってできる流れを吹送流(すいそうりゅう)という。流速ベクトルの先端を結んだとき、「らせん」上に変化する回転系での吹送流をエクマン吹送流、らせん状に変化する流速鉛直構造をエクマンらせん、エクマンらせんが観察できる層(厳密には、流速が表層の1/eになるまでの深さ)をエクマン層と呼ぶ。
エクマン吹送流を、エクマン層程度の深さ(海面から10数メートルくらい)で上下方向に積算してやると、北半球では、結局のところ、風の吹き去る方向に
対して直角右向きの海水輸送量のみが残る。エクマン層下部では流れが弱く、摩擦力も小さくなっている。したがって、エクマン層全体に働く力で重要になるの
は、層全体に働くコリオリ力と、海面に働く風応力だけとなるためである。
講義で見せたエクマン吹送流の実験動画は、地球流体電脳倶楽部「実験室の中の空と海」-北極にて太平洋を想う-から紹介させていただきました。
本講義では、既に学習した支配方程式系を使って、エクマン理論を記述していこう。
無限に広く、無限に深い海洋を考える。y方向に一様な風(風応力をτとする)が吹き続け、定常状態に達したとする。このときの運動方程式は、
定常なので時間変化項を無視は無視できて、
流れが速く、急な空間変化が見込まれるような沿岸域の話ではないので、移流項は無視できて、
海面の凸凹(すなわち圧力分布)は重要ではないので、圧力勾配項は無視できて、
取り扱う現象に壁面境界層は不要なので、水平粘性項は無視できるので、
と書くことができる。ここで、(3)と(4)はz=0(海面)での境界条件であり、y方向にだけ風応力τが働いていることを意味する。
(1)〜(5)の二元常微分方程式を解くと(具体的には、ここ)、
これは、エクマンらせん構造を表す流速の鉛直変化を表している。この流れ(エクマン吹送流)の大きさは、z=-δで表層の1/eとなっている。このδの深度をエクマン深度、表層からエクマン深度までを表層エクマン層と呼ぶ。
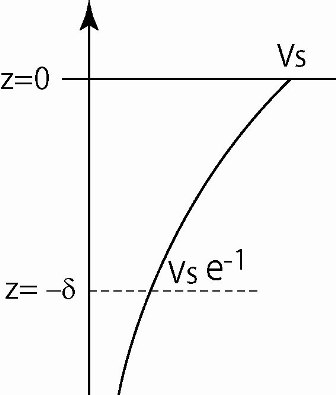
エクマン吹送流の大きさ(√(u2+v2))
エクマン吹送流による海水輸送量は、(1)と(2)を鉛直方向に積分することで得ることができる。すなわち、輸送量は、北半球の場合、風が吹き去る方向の直角右向にτ/(ρf)であり、これをエクマン輸送と呼ぶ。
沿岸湧昇のように海岸に強制されるだけではなく、一般にエクマン輸送量の空間変化は、風応力の空間変化によってもたらされるものである。このようなエクマン輸送の空間変化によって湧昇流や沈降流が生じることをエクマンパンピングと呼ぶ。
【講義で行った実験のムービー】
エクマン輸送の実験です。上から見て反時計周りに回転するレコード盤に水を満たした容器を置き、USBファンで容器の縁に平 行になるよう風を吹かせる。容器に生じる流れを、水面に浮かべたプラスチックビーズで可視化する。風向に対して直角右向きとなるエクマン輸送をビーズの動 きで観察しよう。風向きを逆にすると?
【注】厳密には、ファンの下を過ぎた辺りで最強となる"非定常風"ですが、33回転の場合は慣性周期が一秒足らずなので、半周回る間に概ねエクマン輸送が成立する ようです。なお、プラスチックビーズは比重の軽いポリプロピレン製ですが、沈みがちで風の影響を直接受けにくい重めのHDポリエチレン製(でも、ちっちゃ くて見にくい)を混ぜて、動きに違いがないかチェックしました。この実験系のエクマン深度は、レコード盤の回転速度を33回転にしたとき,鉛直粘性係数を0.01cm2/sとおけば約0.5mm程度。プラスチックビーズの沈下はエクマン深度よりも深くて、その移動方向はエクマン吹送流の鉛直積分値(=エクマン輸送)に近くなるはず。
【解説】
上の画像をクリックするとムービーが始まります。容器の縁を左手に見た方向にファンの風が吹き出す面を向けると、容器の縁から中央に向かっての(=
風向に直角右向きの)エクマン輸送でビーズは中央に集まります。その後にファンを反対に向けると、今度は容器中央から縁に向かってのエクマン輸送となっ
て、ビーズは中央から広がっていきます。後はその繰り返し。*ただし、講義では説明しなかったけれど、この実験系では、北半球を想定して上から見て反時計回りの回転にすると中央から縁に向かう表層の発散流が、時計回りだと逆に収束流が強めになるといったバイアスがあるようです。なぜ?