潮汐と潮流
　
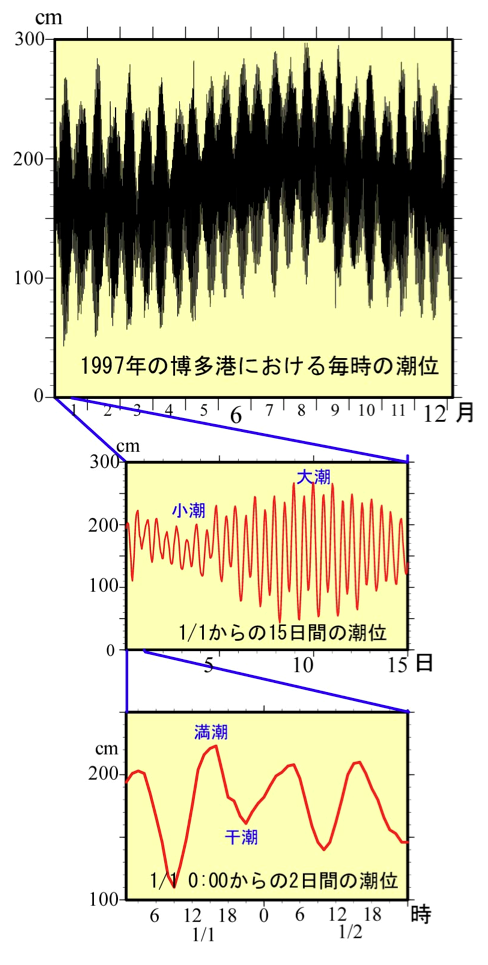
　ま ず、福岡港における潮位変化を見てみよう。一番上の図では、年間を通した潮位の増減に注目してほしい。ほぼ、熱膨張によるものである。中段の図では15日 周期の潮位振幅の増減(大潮(おおしお)・中潮(なかしお)・小潮(こしお))に注目してほしい。下段では一日で二回の干満があること(満潮(高潮)・干 潮(低潮))、そして隣り合う干満の高さ・低さが異なること(日潮不等)に注目。

　熱膨張に伴う潮位の増減は別にして，それ以外の上記潮汐現象や、あるいは潮位が分単位・cm単位で予報できること、はすべて月・太陽・地球に働く力の静力学的な平衡状態から解釈することができる。天体の位置関係から生じる力の静力学的なバランスから、潮汐を生じさせる力（起潮力という）が定義できる。これを静力学的潮汐論(あるいは平衡潮汐論）という。

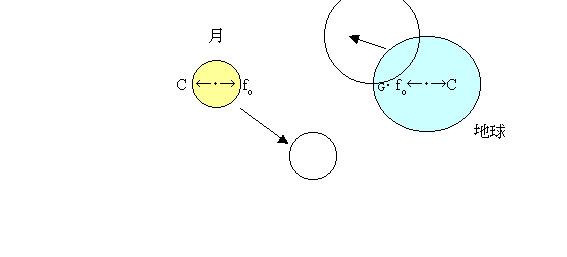
まず、月と地球の間に働く力のバランスを考えてみよう。

いま地球の中心(O)では、月の引力(f_o)は月と地球がその共通重心(G、地球内部にある)のまわりを回るための遠心力(C)と釣り合っている。

このとき、地球表面に働く力をピックアップしてみよう。

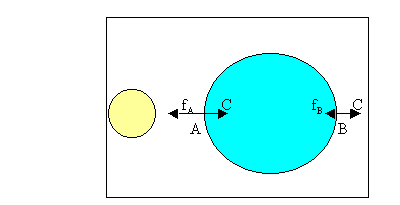
　月に最も近い点Aと最も遠い点Bを考える。ここで遠心力(C)は、共通重心(G)まわりの地球剛体回転の結果として生じるものであるから、地球上ではどこでも同じになる。
　しかし、引力ｆは、月に最も近い点Aで最大、最も遠い点Bで最小になるだろう。結果としてその差し引きが地球表面には働くことになる（この両者の和が０になるのは、地球の中心）。
　この遠心力と引力の差（起潮力)が潮汐(海面の変位)を引き起こす。上では簡単のため、起潮力が地表面に対して垂直なA点とB点で説明した。しかし実際には、起潮力のうち、地表と平行な成分が海水を動かす。鉛直成分は同方向に働く重力に比べ、無視できるほど小さい。


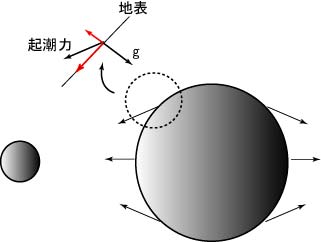
　　　地球上の起潮力の分布と、地表に対して平行な成分、垂直な成分。

地球表面の起潮力の分布は、月との位置関係により、以下の図のように海面をラクビーボールのように変位させる。私たちは、月が南中したときと地球の反対側に行ったとき、１日２回の満潮を経験することになる。

月による起潮力の計算-->講義で

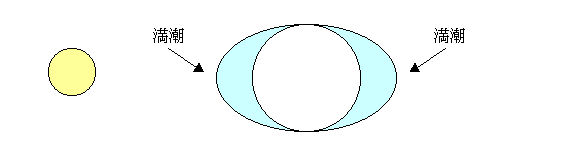
　太陽による起潮力そのものは月に比べて小さいが、太陽と月が一直線上にそろう(新月や満月)とき、両者の起潮力が重なり合って大きな潮汐運動を起こす(大潮)。上弦、下弦の月のときは、両者の起潮力が打ち消しあって、潮汐運動も小さくなる(小潮)。

　私たちが実際の海で経験する潮汐は、月による半日周期の潮汐成分、太陽による半日周期の潮汐成分、あるいは地軸の傾きによる１日周期の潮汐成分(講義で述べる)など、いくつかの潮汐運動の和となる。一つ一つの成分の潮汐運動は、単純な三角関数で表現できる時間変化をするが、和となった潮汐は複雑なものとなる。この一つ一つの潮汐成分を分潮と呼ぶ。