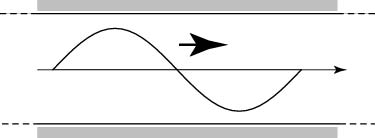
潮汐波は進行波として振る舞い、満潮や干潮になる場所で潮流は最強となる。

動力学的潮汐論
起潮力によって直接に励起される潮汐は、空間スケールの大きな外洋では大きな振幅を持つことが出来る。しかし、内湾や日本海程度の小スケールの海では、無視できる程度の振幅でしかない。
●空間スケール10,000kmの太平洋
→10-7gの起潮力を考える(gは重力加速度)。起潮力とバランスする圧力勾配力をgΔη/Δx (ΔηはΔx離れた2点間の水位差)として、Δxに10,000kmを代入すると、Δηは1m。
●空間スケール100kmとして同様の計算をすると、Δηは1cm。
小さな海で大きな潮汐が実際に観察されるのは、外洋潮汐が重力波(潮汐波と呼ぶ)として入射してくるためである。次の3つのケースに分けて、狭い水路や湾に入射した潮汐波の振る舞いを整理する。
講義で見せた
【ケース1】 潮汐波が狭い一次元水路に入射する場合

潮汐波は進行波として振る舞い、満潮や干潮になる場所で潮流は最強となる。

【ケース2】 入射する潮汐波と閉じた湾奥で反射する潮汐波が重なる場合
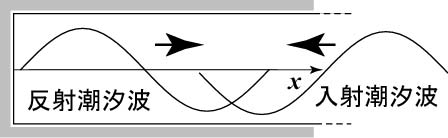
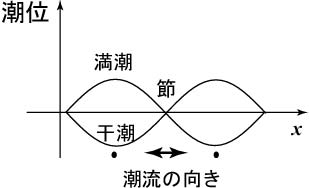
入射潮汐波は湾奥で同位相のまま自由端反射し、図のx軸正方向に伝播する反射潮汐波となる。二つの波の重ねあわせによって定在波となり、潮流が最強となるが潮位変化が無い「節」と、潮流は無いが潮位変化の振幅が最大の「腹」が湾内に形成される。
【ケース3】 長さがLの湾で定在波となる場合
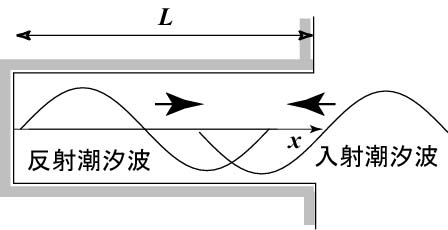
潮汐波の波長λ(位相速度√gH×潮汐周期; Hは水深)が
L=(2m-1)λ/4, m=1,2,3,....
のとき、湾内の潮汐振幅は(非粘性の場合に)無限大になる。共振潮汐。
(注)固定端反射する縦波(音波など)の共鳴条件は、L=mλ/2,
m=1,2,3,...
Bay of Fundyの干満(YouTube)