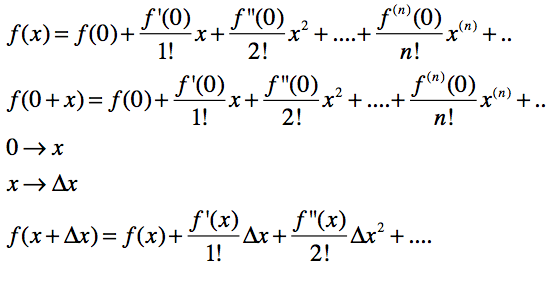
海洋物理学の準備
流体の運動方程式と連続式

　海洋や大気(すなわち"流体")の運動を記述するには、
(1)運動方程式(Navier-Stokes[ナビエ・ストークス]式)
(2)連続式
(3) (海洋の場合は)水温と塩分の保存式
(4) 状態方程式(2.海水の物性と水塊分布で学習済み)
が必要です。この講義では今後の海洋物理学の準備のため、(1)から(3)を導出していきます。

　そのために、テーラー(マクローリン)展開は、知っておいてね。上から順に、ちょっとずつ変形して、この講義では一番下の形を使います。

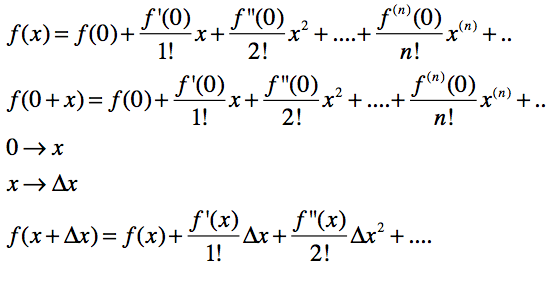
　講義では、静水圧近似(長波近似）とブシネスク近似を使って運動方程式を導出します。それぞれに近似については講義で説明します。
　また、以下の積分公式は余裕で知っているものとして講義します。

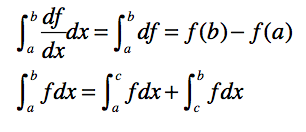
　(1)から(4)の"支配方程式"は、「非線型の6元連立偏微分方程式＋状態方程式」というオソロシゲなものになりますが、もちろん解析的には解けず、主要な項を取り出して支配方程式を単純化するか、あるいはコンピュータ・シミュレーションによって近似解(数値解といいます)を求めます。また、これ以降の講義では、もっと簡単化して取り扱いますから、安心してください。

　でも見方を変えれば、このページに張り付けられる程度の量の方程式で、過去も現在も未来でも、雲の動きや風や海流、そして川の流れなど何でも、流体の振る舞いが統一的に記述できちゃうなんて、なんだか、すごいことだと思いませんか。

以下，地球流体では東向きをxの正方向、北向きをｙの正方向にすることが多いようです。また，海面(静水面)から鉛直上向きをｚの正方向とします。それぞれの方向の流速がu,v,wです。圧力はPでｆはコリオリパラメータ、密度はρで、上二つの最後の二項にかかっている係数は粘性係数です。

(1) 運動方程式(Navier-Stokes[ナビエ・ストークス]式)

　運動量の保存式です。鉛直方向の運動量保存式から、三番目の静水圧方程式は導出されます。

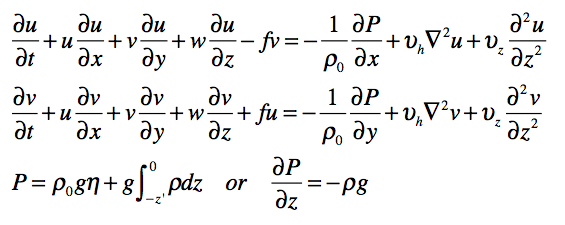
(2) 連続式

　質量(体積)の保存式です。下は非圧縮性流体に対して適用されます。

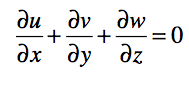
(3) 海洋の場合は)水温と塩分の保存式

　水温(T)と塩分(S)の移流・拡散方程式です。

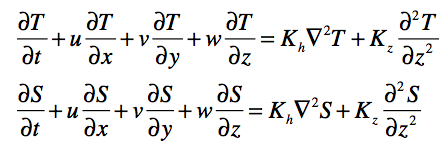
(4) 状態方程式(2.海水の物性と水塊分布で学習済み)

●流体の状態は(1)のナビエ・ストークス式の各項の大きさの比によって記述できます。

　たとえば、移流項(左辺2,3,4項)の大きさは、U²/Lと表現できます。ここで、Uは流速のおおよその大きさで、Lは現象の空間スケールです。たとえば、円柱周りに流れが当たってかき乱される「現象」を見る場合、円柱の直径がLになります。次に、粘性項(右辺2,3項)の大きさはνU/L²(良いフォントがないけどνは"にゅー"で粘性係数)で、移流項の大きさを粘性項の大きさで割ると、
Re＝UL/ν
となり、これをレイノルズ数と呼んでいます。

　レイノルズ数が小さいときは、粘性が移流よりも効いた整然とした流れ(層流)となり、2000～6000よりも大きくなると、移流項が効いた乱雑な流れ(乱流)となります。

　タバコから立ち上る煙は、最初は速度が0で、次第に加速してゆきます。したがって最初はレイノルズ数も小さく、整然と立ち上る煙は層流の状態にあります。煙が上昇するに従って加速すると、レイノルズ数も大きくなって、乱流状態に遷移します。

＊喫煙所でタバコを吸ってた黒TシャツのS君(博士課程三年)を撮影するといった精密な実験なので、少しわかりにくいです。